Cut the shape into two equal parts

How to split a shape into two equal parts. Splitting on checkered paper

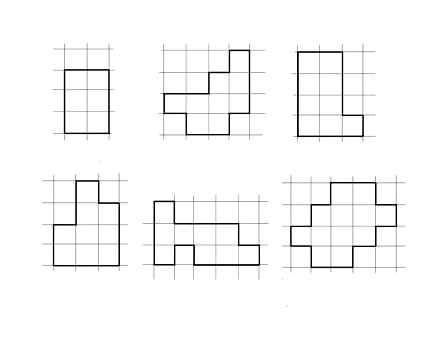
This is actually a simplified version of the Catamino game, requiring only checkered paper and a pencil. Such tasks are often found in textbooks and tasks of olympiads for younger students. It is necessary to divide the figure drawn by the cells into a given number of identical parts.

These tasks are suitable for a very wide age range, starting from three to four years. But don’t abuse them. they end up boring. Most likely, it is worth dwelling on the complexity of 4-5 parts, 4-5 cells in each.

Your kids may need more simple tasks. They are very easy to compose: you just need to go “from the answer”. those. take tartan paper, choose the shape of the figurine (“part”) from several cells and draw several such figures next to each other, “blinding” them together. (It would be nice not to confuse the figures with their mirrored reflections.) It doesn’t matter if it turns out that the problem has two or more solutions. It means that you need to find at least one (or all). Draw the outline of the “monster” you have on a blank sheet of checkered paper. task ready.

In the understanding of mathematics tutors and teachers of various electives and circles, a selection of entertaining and developing geometric cutting problems is offered. The purpose of using such tasks by the tutor in his classes is not only to interest the student with interesting and effective combinations of cells and figures, but also to form in him a sense of lines, angles and shapes. The set of tasks is focused mainly on children in grades 4-6, although it is possible to use it even with high school students. The exercises require students to have a high and steady concentration of attention and are great for developing and training visual memory. Recommended for mathematics tutors preparing students for entrance exams to mathematics schools and classes that have special requirements for the level of independent thinking and creativity of the child. The level of the problems corresponds to the level of the entrance olympiads in the “second school” lyceum (second mathematical school), small Mechmatist of Moscow State University, Kurchatov school, etc.

Equal Parts

Math tutor’s note: In some of the solutions to problems that you can see by clicking on the corresponding index, only one of the possible examples of cutting is indicated. I fully admit that you may end up with some other correct combination. don’t be afraid of that. Check carefully the solution of your mind and if it satisfies the condition, then feel free to tackle the next task.

1) Try cutting the figure shown in the figure into 3 equal parts:

Small shapes are very similar to the letter T

2) Now cut this shape into 4 equal parts:

Math Tutor’s Tip: It’s easy to guess that small figures will consist of 3 cells, and there will not be many figures of three cells. There are only two types of them: a corner and a rectangle 1 × 3.

3) Cut this shape into 5 equal parts:

Find the number of cells that each such figure consists of. These figures look like the letter G.

4) And now you need to cut a figure of ten cells into 4 rectangles (or squares) unequal to each other.

Math tutor’s instruction: Select a rectangle, and then try to write three more in the remaining cells. If it doesn’t work, then change the first rectangle and try again.

5) The task becomes more complicated: you need to cut the figure into 4 figures of different shapes (not necessarily into rectangles).

Math tutor’s tip: first draw separately all types of figures of different shapes (there will be more than four of them) and repeat the method of iterating through the options as in the previous task. :

6) Cut this figure into 5 figures of four cells of different shapes so that only one green cell is painted over in each of them.

Math Tutor’s Tip: Try to start cutting at the top edge of the given shape and you will know how to proceed right away. :

7) Based on the previous problem. Find how many figures of various shapes, consisting of exactly four cells, are there? The figures can be twisted, rotated, but you cannot lift the table (from its surface), on which it lies. That is, the two given figures will not be considered equal, since they cannot be obtained from each other by turning.

Math tutor’s tip: Study the solution to the previous problem and try to imagine the different positions of these shapes when turning. It is not hard to guess that the answer in our problem will be the number 5 or more. (In fact, even more than six). There are 7 types of described figures in total.

8) Cut a square of 16 cells into 4 equal-shaped pieces so that each of the four pieces contains exactly one green cell.

Math Tutor’s Tip: The look of the little figures is not a square or rectangle, or even a four-square corner. So what shapes should you try to cut?

9) Cut the depicted figure into two parts so that the resulting parts can be folded into a square.

Math tutor’s tip: There are 16 squares in the figure, which means that the square will be 4 × 4 in size. And somehow you need to fill the window in the middle. How to do it? Could it be some kind of shift? Then, since the length of the rectangle is equal to the odd number of cells, the cutting should be done not with a vertical cut, but along a broken mowing line. So that the upper part is cut off on one side of the middle cells, and the lower part on the other.

10) Cut a 4 × 9 rectangle in two so that you can add a square as a result.

Math Tutor’s Tip: There are 36 cells in a rectangle. Therefore, the square will be 6 × 6. Since the long side consists of nine cells, three of them must be cut off. How will this cut go further??

11) The cross of five cells, shown in the figure, needs to be cut (you can cut the cells themselves) into parts from which a square could be folded.

Math tutor’s tip: It is clear that no matter how we cut the cells along the lines, we will not get a square, since there are only 5 cells. This is the only problem in which it is allowed to cut not by cells. However, it would still be good to leave them as a guideline. for example, it is worth noting that we somehow need to remove the indentations that we have. namely, in the inner corners of our cross. How would you do it? For example, cutting off some protruding triangles from the outer corners of the cross.

“Squares of shapes geometry”. in). which will be equal to the area of ​​the figure composed of figures A and G. Pythagorean theorem. Squares of various shapes. Shapes of equal area. Equal pieces have equal areas. The figures are divided into squares with a side of 1 cm. Rectangular triangles. Shapes with equal areas are called equal. Solve the rebus.

“Tolstoy Two Brothers”. I’m ready to go. The main idea of ​​the tale. And now walking is in place, Left. right, stop once or twice. ” Two brothers”. I want to learn. We’ll sit down at our desks, together we’ll get down to business again. My attention is growing. Let’s get acquainted with the work of L.N. Tolstoy and the work “Two Brothers”. We will be lost for nothing. we will be lost in vain We will remain with nothing, we will remain with nothing.

“Two Captains Kaverin”. Sanya lives in Ensk with his parents and sister Sasha. The novels “Open Book” and “Two Captains” have been filmed several times. Fock “under the command of Georgy Sedov, on the schooner” St. V.A. Kaverin. The expedition did not return. The first story “Chronicle of the city of Leipzig. Nikolai Antonovich, Katya’s great-uncle turns out to be ungrateful.

“Human’s figure”. The word “proportion” in translation from Latin means “ratio”, “proportionality”. Main Body (belly, chest) Didn’t pay attention Head, face, hands. Renaissance. Proportions. Artists and architects of the 20th century. 5. Examples of different movements. Ancient Egypt. The skeleton plays the role of a skeleton in the structure of the figure.

“The likeness of figures.” Animals. Materials from the Internet were used. Similarity in our life. Geometry. If you change (increase or decrease) all the dimensions of a flat figure in the same number of times (similarity ratio), then the old and new figures are called similar. Similar triangles. Plants. Similarity surrounds us. Similarity of flat figures.

“Interference of two waves”. Interference. Waves from different sources are not coherent. The razor is held in the water by the surface tension of the oil film. Interference The wave path difference depends on the film thickness. Interference of mechanical sound waves. What is the optical phenomenon? Cause? Different colors of light correspond to different wavelength intervals.

Presentation for a lesson in visual geometry in grade 5. Focused on a textbook for the educational institution “Visual geometry”, grades 5-6 / IF Shaprygin, LN Erganzhieva. Publisher: Bustard, 2015.

Basic concept: equality of shapes. Subject results: depict equal figures and justify their equality; construct given figures from flat geometric figures; create and manipulate an image: dismember, rotate, combine, superimpose. Metasubject results: the development of imaginative thinking, design skills, the ability to anticipate the result, the formation of communication skills.

Personal results: development of cognitive activity; instilling a taste for mental work. Intrasubject and interdisciplinary connections: planimetry (equality of figures, symmetry, area, equal size and equal composition), geometric combinatorics, drawing, technology.

This lesson. the first of two on this topic.

This lesson covers cutting tasks. The goal of the decider is to cut the specified figure into two or more equal parts. Often, for simplicity, this figure is divided into cells. In these problems, the concept of equality of shapes is implicitly introduced (shapes that coincide when superimposed are called equal). This definition is also used to check the equality of the resulting figures.

Portal for the student. Self-preparation

View the contents of the document “Tasks for cutting and folding shapes. Lesson 1”

Purpose: to consolidate the ability to solve cutting problems.

This proverb warns you against haste in solving problems.

A given figure, which is divided into equal cells for ease of use, must be cut into two or more parts.

If these parts can be superimposed on one another so that they coincide (while the figures are allowed to be turned over), then the problem is solved correctly.

Local land trader

grabbed a piece of unusual land for the occasion

forms (he hoped to profitably sell it in parts).

The square consists of 16 identical cells,

4 of them are painted over. Cut the square into

4 equal parts so that in each of them

there was only one filled cell.

How to Split Shapes | Illustrator CC Tutorial

The cage can take any place in each part.

Cut the rectangle into 4 equal pieces,

(apply as many ways as possible).

The presentation offers only 4 ways to solve this problem. Perhaps the students will suggest other ways. they also need to be considered in class.

Make shapes out of them. How many of them turned out?

Take four identical squares. Make shapes out of them.

There are 12 pentomino elements in total

Cut into two equal parts, part one

Cutting problems are an area of ​​mathematics where, as they say, the mammoth was not lying around. Many separate problems, but in fact there is no general theory. Apart from the well-known Boyai-Gerwin theorem, there are practically no other fundamental results in this area. Uncertainty is the eternal companion of cutting tasks. We can, for example, cut a regular pentagon into six pieces that can be folded into a square; however, we cannot prove that five parts would not be enough for this.

With the help of clever heuristics, imagination and half a liter, we sometimes manage to find a specific solution, but, as a rule, we do not have the appropriate tools to prove the minimality of this solution or its nonexistence (the latter, of course, refers to the case when we did not find a solution) This is sad and unfair. And once I took a blank notebook and decided to restore justice on the scale of one specific task: cutting a flat figure into two equal (congruent) parts. As part of this series of articles (there will be three of them, by the way), you and I, comrades, will consider this funny polygon, shown below, and try to impartially figure out whether it is possible to cut it into two equal figures, or not.

Introduction

To begin with, let’s refresh the school geometry course and remember what equal shapes are. Yandex helpfully suggests:

Two figures on a plane are called equal if there is a movement that mutually transfers one figure to another.

Now let’s ask Wikipedia about movements. She will tell us, first, that motion is a plane transformation that preserves the distances between points. Secondly, there is even a classification of movements on a plane. They all belong to one of the following three types:

• Parallel transfer
• Turn
• Sliding symmetry (here, for the sake of convenience and benefit, I include mirror symmetry, as a degenerate case where the parallel transfer is performed to the zero vector)

Let’s introduce some notation. We will call the cut figure figure A, and the two hypothetical equal figures into which we supposedly can cut it, call B and C, respectively. The part of the plane that is not occupied by the figure A, we will call the area D. In those cases when a specific polygon from the picture is considered as the cut figure, we will call it A0.

So, if figure A can be cut into two equal parts B and C, then there is a movement that translates B into C. This movement can be either a parallel translation, or a rotation, or sliding symmetry (from this moment on, I no longer stipulate, that mirror symmetry is also considered to be sliding). Our decision will be built on this simple and, I would even say, obvious, basis. In this part we will look at the simplest case. parallel transfer. Rotation and sliding symmetry will fall into the second and third parts, respectively.

Case 1: parallel transfer

Parallel transfer is specified by the only parameter. the vector by which the shift occurs. Let’s introduce a few more terms. A straight line parallel to the shift vector and containing at least one point of the figure A will be called secant. The intersection of the secant line and the figure A will be called cross-section. The secant with respect to which the figure A (minus the section) lies entirely in one half-plane will be called border.

Lemma 1. The section by the boundary must contain more than one point.

Proof: obvious. Well, or more fully: we will prove it by contradiction. If this point belongs to figure B, then its form (that is, the point to which it goes during the parallel transfer) belongs to the figure C = the image belongs to the figure A = the image belongs to the section. Contradiction. If this point belongs to the figure C, then its prototype (the point, which, in the case of a parallel transfer, goes to it) belongs to figure B, and then similarly. It turns out that there must be at least two points in the section.

Guided by this simple lemma, it is easy to understand that the sought-for parallel translation can occur only along the vertical axis (in the current orientation of the picture) If it were in any other direction, at least one of the boundary sections would consist of a single point. This can be understood by mentally rotating the displacement vector and seeing what happens to the boundaries. To eliminate the case of vertical parallel translation, we need a more sophisticated tool.

Lemma 2. The inverse image of a point located on the boundary of the figure C is either on the boundary of the figures B and C, or on the boundary of the figure B and the domain D.

Proof: Not obvious, but we’ll fix that now. Let me remind you that the boundary point of a figure is a point such that as close to it there are points that belong to the figure as well as points that do not belong to it. Accordingly, near the boundary point (let’s call it O ‘) of the figure C, there are both points of the figure C and other points belonging either to the figure B or to the domain D. Only the points of the figure B can be inverse images of the points of the figure B. Therefore, arbitrarily close to the preimage of the point O ‘(it would be logical to call it point O) there are points of the figure B. The preimages of the points of the figure B can be any points that do not belong to B (that is, either the points of the figure C, or the points of the region D). Similarly, for points of the domain D. Therefore, arbitrarily close to the point O there are either points of the figure C (and then the point O will be on the boundary of B and C), or points of the domain D (and then the inverse image on the boundary of B and D). If you can get through all these letters, then you will agree that the lemma is proved.

Theorem 1. If the section of the figure A is a segment, then its length is a multiple of the length of the displacement vector.

Proof: consider the “distant” end of this segment (that is, the end whose inverse image also belongs to the segment). This end, obviously, belongs to the figure C and is its boundary point. Consequently, its preimage (by the way, also lying on a segment and spaced from the image by the length of the shift vector) will be either on the boundary between B and C, or on the boundary between B and D. If it is on the boundary between B and C, then we also take its preimage We will repeat this operation until the next preimage ceases to be on the boundary C and ends up on the boundary D. and this will happen just at the other end of the section. As a result, we get a chain of preimages that divide the section into a number of small segments, the length of each of which is equal to the length of the shift vector. Consequently, the section length is a multiple of the length of the shear vector, p.t.d.

Corollary from Theorem 1. Any two sections that are segments must be commensurable.

Using this corollary, it is easy to show that vertical parallel translation also disappears.

Indeed, a section of times has a length of three cells, and a section of two is three minus the root of two in half. Obviously, these quantities are incommensurable.